Graph Colouring

Graph Coloring Problem

Graph coloring (also called vertex coloring) is a way of coloring a graph’s vertices such that no two adjacent vertices share the same color. This post will discuss a greedy algorithm for graph coloring and minimize the total number of colors used.

For example, consider the following graph:

Graph coloring

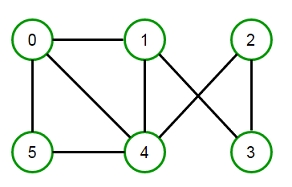
We can color it in many ways by using the minimum of 3 colors.

Please note that we can’t color the above graph using two colors.

Before discussing the greedy algorithm to color graphs, let’s talk about basic graph coloring terminology.

K–colorable graph:

A coloring using at most k colors is called a (proper) k–coloring, and a graph that can be assigned a (proper) k–coloring is k–colorable.

K–chromatic graph:

The smallest number of colors needed to color a graph G is called its chromatic number, and a graph that is k–chromatic if its chromatic number is exactly k.

Brooks’ theorem:

Brooks’ theorem states that a connected graph can be colored with only x colors, where x is the maximum degree of any vertex in the graph except for complete graphs and graphs containing an odd length cycle, which requires x+1 colors.

Greedy coloring considers the vertices of the graph in sequence and assigns each vertex its first available color, i.e., vertices are considered in a specific order v1, v2, … vn, and vi and assigned the smallest available color which is not used by any of vi’s neighbors.

Greedy coloring doesn’t always use the minimum number of colors possible to color a graph. For a graph of maximum degree x, greedy coloring will use at most x+1 color. Greedy coloring can be arbitrarily bad; for example, the following crown graph (a complete bipartite graph), having n vertices, can be 2–colored (refer left image), but greedy coloring resulted in n/2 colors (refer right image).

#include <iostream>
#include <vector>
#include <unordered_map>
#include <set>
using namespace std;
 
// Data structure to store a graph edge
struct Edge {
    int src, dest;
};
 
class Graph
{
public:
    // a vector of vectors to represent an adjacency list
    vector<vector<int>> adjList;
 
    // Constructor
    Graph(vector<Edge> const &edges, int n)
    {
        // resize the vector to hold `n` elements of type `vector<int>`
        adjList.resize(n);
 
        // add edges to the undirected graph
        for (Edge edge: edges)
        {
            int src = edge.src;
            int dest = edge.dest;
 
            adjList[src].push_back(dest);
            adjList[dest].push_back(src);
        }
    }
};
 
// Add more colors for graphs with many more vertices
string color[] =
{
    "", "BLUE", "GREEN", "RED", "YELLOW", "ORANGE", "PINK",
    "BLACK", "BROWN", "WHITE", "PURPLE", "VOILET"
};
 
// Function to assign colors to vertices of a graph
void colorGraph(Graph const &graph, int n)
{
    // keep track of the color assigned to each vertex
    unordered_map<int, int> result;
 
    // assign a color to vertex one by one
    for (int u = 0; u < n; u++)
    {
        // set to store the color of adjacent vertices of `u`
        set<int> assigned;
 
        // check colors of adjacent vertices of `u` and store them in a set
        for (int i: graph.adjList[u])
        {
            if (result[i]) {
                assigned.insert(result[i]);
            }
        }
 
        // check for the first free color
        int color = 1;
        for (auto &c: assigned )
        {
            if (color != c) {
                break;
            }
            color++;
        }
 
        // assign vertex `u` the first available color
        result[u] = color;
    }
 
    for (int v = 0; v < n; v++)
    {
        cout << "The color assigned to vertex " << v << " is "
             << color[result[v]] << endl;
    }
}
 
// Greedy coloring of a graph
int main()
{
    // vector of graph edges as per the above diagram
    vector<Edge> edges = {
        {0, 1}, {0, 4}, {0, 5}, {4, 5}, {1, 4}, {1, 3}, {2, 3}, {2, 4}
    };
 
    // total number of nodes in the graph (labelled from 0 to 5)
    int n = 6;
 
    // build a graph from the given edges
    Graph graph(edges, n);
 
    // color graph using the greedy algorithm
    colorGraph(graph, n);
 
    return 0;
}

Output: The color assigned to vertex 0 is BLUE The color assigned to vertex 1 is GREEN The color assigned to vertex 2 is BLUE The color assigned to vertex 3 is RED The color assigned to vertex 4 is RED The color assigned to vertex 5 is GREEN

The time complexity of the above solution is O(V × E), where V and E are the total number of vertices and edges in the graph, respectively.

Applications of graph coloring:

The problem of coloring a graph arises in many practical areas such as pattern matching, designing seating plans, scheduling exam timetable, solving Sudoku puzzles, etc.