Rat in a Maze

A Maze is given as N*N binary matrix of blocks where source block is the upper left most block i.e., maze[0][0] and destination block is lower rightmost block i.e., maze[N-1][N-1]. A rat starts from source and has to reach the destination. The rat can move only in two directions: forward and down.

In the maze matrix, 0 means the block is a dead end and 1 means the block can be used in the path from source to destination.

Following is an example maze.

 Gray blocks are dead ends (value = 0).

Following is a binary matrix representation of the above maze.

{1, 0, 0, 0}
{1, 1, 0, 1}
{0, 1, 0, 0}
{1, 1, 1, 1}

Following is a maze with highlighted solution path.

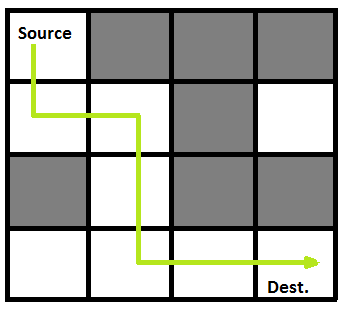
Following is the solution matrix (output of program) for the above input matrix.

{1, 0, 0, 0}
{1, 1, 0, 0}
{0, 1, 0, 0}
{0, 1, 1, 1}
All entries in solution path are marked as 1.

Solving one piece at a time, and removing those solutions that fail to satisfy the constraints of the problem at any point of time (by time, here, is referred to the time elapsed till reaching any level of the search tree) is the process of backtracking.

Approach: Form a recursive function, which will follow a path and check if the path reaches the destination or not. If the path does not reach the destination then backtrack and try other paths.

Algorithm:

1. Create a solution matrix, initially filled with 0’s.

2. Create a recursive function, which takes initial matrix, output matrix and position of rat (i, j).

3. if the position is out of the matrix or the position is not valid then return.

4. Mark the position output[i][j] as 1 and check if the current position is destination or not. If destination is reached print the output matrix and return.

5. Recursively call for position (i+1, j) and (i, j+1).

6. Unmark position (i, j), i.e output[i][j] = 0.